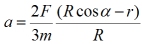|
NEW!
Pan Hieronim pokazuje taką „sztuczkę”: na szpulę o wewnętrznym promieniu r i promieniu zewnętrznym R jest nawinięty giętki pas. Pan Hieronim, odpowiednio unosząc albo opuszczając ten pas, „pociąga” szpulkę do siebie, ale ta toczy się raz w prawo, raz w lewo, w zależności od pochylenia pasa.
Dlaczego? Zobacz jak rozwiązuje się tego typu problemy
|
Doświadczenie wygląda tak:
JW Player goes here
Autorzy: mgr Krzysztof Służewski (KS16), prof. Grzegorz Karwasz
"Sztuczka" Pana Hieronima (mgr Hieronima Ratajczaka, emerytowanego dziś pracownika Pracowni Pokazów Fizycznych UMK) opiera się na współdziałaniu dwóch sił - ciągnącej szpulę (w prawo na filmie) i siły tarcia statycznego (działającej w tym przypadku w lewo). Dwie siły (a właściwie momenty tych sił) tak się sumują, że raz szpula przyspiesza w prawo, raz w lewo, w zależności od kąta przyłożenia siły ciagnącej.
Przyjrzyjmy się temu doświadczeniu dokładniej (kliknij, żeby odkryć tekst)
Przy obniżaniu taśmy szpula toczy się w prawo, przy jej podnoszeniu - w lewo. Dla pewnego kąta granicznego φ szpula nie toczy się. Sytuację przedstawia poniższy rysunek (kliknij, żeby powiększyć).
Uwaga o sile tarcia (wektor zielony). Z zadania poprzedniego (3.8. "Kot i szpulka nici") wiemy, że w przypadku zaczepienia linki pod środkiem szpuli, siła tarcia statycznego działa w lewo. Nie wiemy z góry, ile ona wynosi. Wiemy jedynie, że jej maksymalna wartość jest równa iloczynowi ciężaru szpuli i współczynnika tarcia statycznego. W tym zadaniu problem jest jeszcze bardziej złożony, gdyż składowa pionowa siły ciągnącej zmniejsza siłę nacisku na podłoże (siła nacisku jest mniejsza niż ciężar szpuli). Dla uproszczenia, na wszystkich rysunkach siła tarcia zaznaczona jest taka sama.
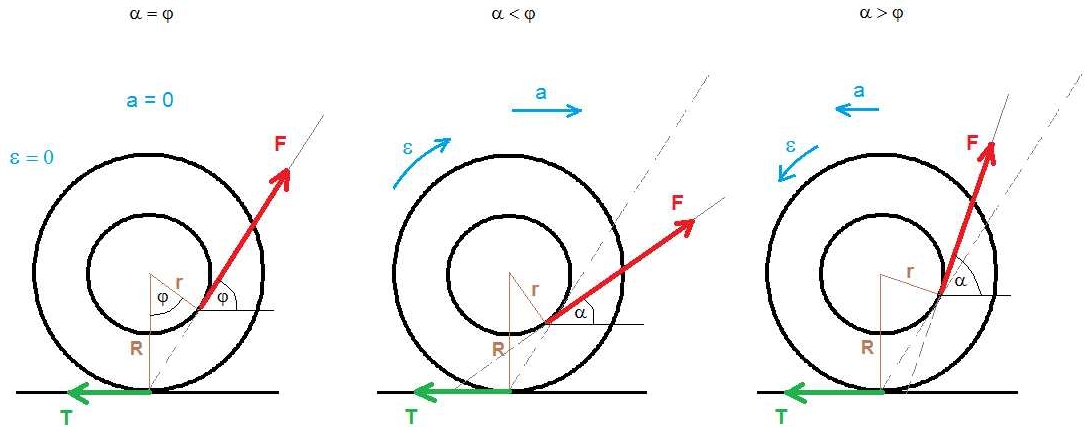
Po lewej widzimy sytuację kąta granicznego (szpulka nie toczy się, a przy użyciu większej siły przemieszcza się przez poślizg, zob. powyżej uwagę o sile tarcia). Na środkowym rysunku szpulka porusza się w prawą stronę , a na prawym w lewą.
Jak pokażemy dalej, w przypadku kąta granicznego cosφ=r/R.
Policzmy kąt graniczny (kliknij, żeby odkryć tekst)
(rozważamy rysunek 2: siły i przyspieszenie są dodatnie, jeśli sa skierowane w prawo)
Z II zasady dynamiki Newtona mamy równanie:
Fcosα - T = ma → T = Fcosα - ma (1)
F jest siłą wymuszającą ruch (zaznaczoną na czerwono na rysunkach), T jest siłą tarcia statycznago, m to masa szpuli natomiast a przyspieszenie, z jakim sie porusza.
Analogicznie dla ruchu obrotowego (rozważamy momenty sił, zamiast sił) mamy:
TR - Fr = Iε (2)
r jest promieniem, na który nawinięta jest taśma, R to promień, po którym toczy się szpula, I to moment bezwładności szpuli, a ε - jej przyspieszenie kątowe.
Na rysunku 2 siła tarcia T ma taki kierunek, że przyspieszenie kątowe przez nią wywołane jest dodatnie - prędkość kątowa rośnie. Stąd znak plus przy momencie siły TR (a znak minus przy Fr) Korzystając z rysunku 3, należałoby zmienić znaki sił w równaniu (1) i konsekwentnie znaki momentów siły w równaniu (2), albo znaki przyspieszeń.
Siły F i T działają prostopadle do promieni r i R, dlatego momenty sił zapisujemy jako "zwykłe" iloczyny algebraiczne.
Przyjmijemy (w przybliżeniu pełnego walca o promieniu R), że moment bezwładności szpuli wynosi 1/2mR2 (w rzeczywistości jest on nieco mniejszy)
I=½mR2, natomiast ε=a/R (3)
Po podstawieniu wyrażenie (2) będzie miało wartość:
Tr - Fr = ½mRa
Po podstawieniu T wyrażeniem z pierwszego wzoru i kilku przekształceniach otrzymujemy:
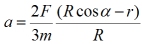
Dla kąta granicznego przyspieszenie a wynosi zero. Mogą zachodzić warunki:
• siła wymuszająca F wynosi zero (odrzucamy - nie interesuje nas ten przypadek)
• masa i promień szpulki są nieskończenie duże (odrzucamy - znamy m i R naszej szpulki)
• nawias Rcosα - r wynosi zero, czyli cosα = r/R (ten sam warunek, który zauważyliśmy na rysunku - o ten przypadek nam chodzi).
Zobaczmy, ile wynosi kąt graniczny φ dla badanej szpulki.
Promień R wynosi 8 cm, a promień r 5,5cm. Podstawiając:
cosφ = 5,5/8 → φ = 47o
Sprawdźmy teraz doświadczalnie, czy obliczony kąt sprawdzi się.
JW Player goes here
W doświadczeniu ze szpulą kota i nicią (3.8 w "Zbirce) sytuacja jest podobnie skomplikowana. W zależnosci od punktu przyłożenia siły ciągnącej siła tarcia statycznego zmienia swą wartość, zob. rys. w zadaniu 3.8. Co więcej, jeśli nić jest zaczepiona powyżej osi, w odległości co najmniej R/2, siła tarcia zmienia kierunek, na zgodny z siłą ciagnącą. Tak! tarcie w trakcie toczenia się jest tarciem statycznym, a tarcie statyczne działa zawsze przeciw możliwemu kierunkowi poślizgu.
Spójrzmy na ciała na równi pochyłej. Zaczynają się poruszać, dopiero wtedy, kiedy równia pochylona jest pod odpowiednio dużym kątem. Jednym z głównych czynników, który określa kiedy ciało zaczyna się poruszać jest właśnie siła tarcia statycznego.
JW Player goes here
Spójrzmy teraz na kolejne doświadczenie, które pokaże nam jak jest różnica pomiędzy tarcie statycznym i dynamicznym i od czego te siły zależą.
JW Player goes here
Ciąg dalszy na kolejnej stronie
(C) Koncepcja GK, Tekst KS (i GK), Multimedia - koncepcja, doświadczenia, teksty KS, Multimedia - przygotowanie KS, we współpracy z AK. (C) ZDF 2015