Fizyka dla każdego

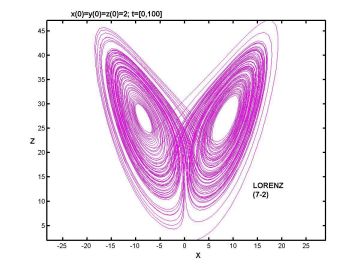
Powyższe równania badał meteorolog pracujący w MIT w USA i wyniki opublikował w słynnej pracy z roku 1963 [1]. Skrzydła motyla stały się szybko ikoną chaosu deterministycznego, a matematycznie, są wizualizacją tzw. dziwnego atraktora. W następnych latach intensywnie szukano układów prostszych od Lorenza. J.C. Sprott z USA, po przebadaniu numerycznym milionów układów równań, znalazł około dwudziestu układów równań prostszych algebraicznie od układu Lorenza. Równania Lorenza zawierają po prawej stronie siedem wyrazów i dwie nieliniowości. Najprostszy układ z chaosem deterministycznym znalazł Sprott i ma on pięć wyrazów i tylko jedną nieliniowość kwadratową. Są to równania postaci [2]:
ẋ=y²-z, ẏ=x-Ay, ż=y, gdzie A jest parametrem kontrolnym.