|
 |
 |
 |
 |
 |
 |
 |
 |
| Przegląd prasy | Dla nauczycieli | Dla młodzieży | Przyroda | Video-fizyka | Fizyka współczesna | Projekt FCHGo | Innowacyjna fizyka | Projekt E4 |
<<< Poprzednia część artykułu <<< Dydaktycznie, i serio 1. Stan nieważkości (czy ogólnie spadku swobodnego, jak skok Felixa Baumgartnera we wrześniu 2012 roku) może być okazją do ciekawych doświadczeń interaktywnych, nawet na poziomie szkoły podstawowej. Autor wypróbował je w serii wykładów dla Uniwersytetów Dziecięcych [8]. Odtworzoną sekwencję rozumowania przedstawiają foto 5 i 6.
Fot. 4. Sekwencja (na drabinie) interaktywnej lekcji autora dla dzieci (6-12 lat) o stanie nieważkości. 2. Zagadnienie nieważkości uzmysławia nam, że nie bardzo rozumiemy, iż prędkość jest wektorem, i że jej zmiana (czyli pochodna po czasie) jest trudna do policzenia. Jeżeli prędkość Stacji Kosmicznej się zmienia (co do kierunku i zwrotu, choć wartość jest stała), to znaczy, że podlega ona przyspieszeniu. Tak! i to jest właśnie przyspieszenie, które nazywamy dośrodkowym. JW Player goes here
Fot. 5. Czy ruch na orbicie jest spadkiem swobodnym? Ależ tak! Misiek (i statek) leciał przed siebie, ale chwilę później już leci nieco w dół; a za chwilę jeszcze bardziej (wektor prędkości – ręka, pozostaje stale prostopadły do wektora wodzącego położenia – kręgosłupa wykładowcy). Foto: K. Służewski. 3. Jeśli obserwujemy przyspieszenie dośrodkowe, to musi działać jakaś siła dośrodkowa. Coś w rodzaju sznura, który ciągnie latający po okręgu kamień. Oczywiście! Tym sznurkiem jest siła grawitacji, która nie pozwala polecieć Stacji w siną dal, prosto przed siebie. 3a. Rozważania o układach nieinercjalnych nie są proste, nawet bez grawitacji. Rozważając obracający się układ odniesienia, z wyliczenia prędkości jako pochodnej wektora położenia a przyspieszenia jako pochodnej wektora prędkości pojawiają się w rozwiązaniu iloczyny wektorowe mające sens przyspieszenia dośrodkowego i Coriolisa. Po pełny wzór odsyłamy Czytelnika np. do angielskiej wersji wikipedi [9]. 4. Pytanie: czy naprawdę w statku kosmicznym nie ma różnic w grawitacji? Oczywiście są: różne obiekty w statku kosmicznym krążą po orbitach o nieco różnych promieniach. Siła grawitacji, gdy działa jako siła dośrodkowa, dla orbity kolistej jest związana z prędkością kątową na orbicie poprzez równanie:
gdzie G jest stałą grawitacji, M – masą Ziemi, r – promieniem orbity. Tak więc, wewnątrz statku kosmicznego obiekty leżące (w właściwie „wiszące” nieważko) dalej od Ziemi niż r spóźniają się nieco w locie na orbicie. Aby temu zapobiec, można je przywiązać; jeśli przywiążemy je na sprężynkach, zmierzymy działające siły. >>>> Kolejna część artykułu >>>> [8] G. Karwasz, Skok z kosmosu, wykład interaktywny (2012) http://dydaktyka.fizyka.umk.pl/nowa_strona/?q=node/277
>>>> Kolejna część artykułu >>>>
|
|||||||










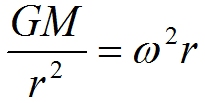 (1),
(1),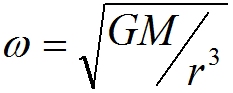 .
.