|
 |
 |
 |
 |
 |
 |
 |
 |
| Przegląd prasy | Dla nauczycieli | Dla młodzieży | Przyroda | Video-fizyka | Fizyka współczesna | Projekt FCHGo | Innowacyjna fizyka | Projekt E4 |
3/7 Wstęp
Sumowanie momentu pędu możemy pokazać w klasie lub na wykładzie, jednak jest to dość niebezpieczne doświadczenie. Rozkręcamy koło rowerowe (oś obrotu skierowana góra-dół) i podajemy uczniowi/studentowi (silnemu!), siedzącemu na krześle obrotowym. Jego zadaniem jest obrócenie koła o 180 stopni. Działając zewnętrzna siłą na koło studentka zmienia moment pędu koła - nic więc dziwnego, że po przekręceniu koła sama (wraz z kołem i jego osią) zaczyna obracać się. Kierunek obrotu studentki, jest zgodny z początkowym kierunkiem obrotu koła. Zasada zachowania momentu pędu musi byc zachowana. Po obróceniu koło rowerowe porusza się wolniej niż bezpośrednio po rozkręceniu. Ponowne obrócenie koła o 180 stopni daje już mniejszy efekt. Koło rowerowe kręci sie już wolniej, dodatkowo przeciwnie do obrotu studentki. JW Player goes here
A tu kolejny ciekawy bączek – szeroki na dole, wąski u góry. Środek ciężkości z całą pewnością jest niżej niż jego połowa wysokości. Wydawałoby się, że możemy z góry przewidzieć sposób jego poruszania – będzie kręcił się wokół własnej osi, jak zwykły bączek, ewentualnie może będzie bardziej się kiwał na boki. Rozkręcamy go i … zaskoczenie. Bączek kładzie się na boku i po chwili staje na nóżce, która przed chwilą była u góry. Warto zwrócić uwagę, że dla obserwatora z zewnątrz kierunek obrotów bąka sie nie zmnienia, ale dla obserwatora związanego z bąkiem kierunek ten sie odwraca. JW Player goes here
Wektor momentu pedu L za zaczepiamy na osi wirowania. Z punktu widzenia bąka jego kierunek przez zały czas sie zmienia aż do momentu, kiedy ztaje na nóżce. Jeżeli bąk wiruje tak, jak na rysunku ponizen to Moment pędu L i prędkość kątowa
Moment pędu definiuje się tak: L=I gdzie I jest momentem bezwładności, a Już przed naszą erą wiedziano, że oś Ziemi nie wskazuje przez cały czas tego zamego kierunku. Wykreśla stożek zamykający się raz na ok. 26 tys. lat. Zjawisko to nazywamy precesja osi ziemskiej. Wiedział o tym też Kopernik. Wyróżniał 3 ruchy Ziemi: wirowanie, obieg dookoła Słońca i przesuwanie się punktów równonocy. Na podstawie obserwacji obliczył czas jednego, pełnego cyklu na 25816 lat (rok platoński).
Ruch precesyjny zauważamy oczywiście również w ruchu małych bączków (w praktyce często nie da się go wykluczyć). Poniżej przedstawiamy doswiadczenie. na rozkręcony bąk działamy przez krótki czas siłą prostopadłą do osi obrotu. Bąk nie wychyla się wcale w kierunku działania siły, ale w kierunku prostopadłym zaróno do niego, jak i do osi obrotu zabawki. JW Player goes here
Poniżej przedstawiamy precesję giroskopu (czytaj: „żyroskopu”). Jego precesję powoduje niezrównoważona siła grawitacji ziemskiej i opory ruchu. Kierunek precesji jest zgodny z kierunkiem wirowania giroskopu.
>>>>>>Kolejna część artykułu>>>>>> Filmy - Bączki: składanie kolorów, z bezwładną masą w środku, magnetyczne, precesyjno - nutacyjne, grające, świecące, grająco-świecące, inne |
|||||||



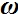 wskazują ten sam kierunek.
wskazują ten sam kierunek.