Balonik naciągamy na otwór butelki. Możemy balonik zamocować do butelki nitką lub za pomocą tzw. gumki recepturki. Następnie balonik z butelką wkładamy do szklanego naczynia wypełnionego zimną wodą. Nie obserwujemy żadnych zmian. Następnie balonik wkładamy do gorącej wody. Możemy wówczas zaobserwować, że balonik jest coraz większy – jak gdyby jakiś mały niewidzialny krasnoludek go nadmuchał. Tym „krasnoludkiem” jest oczywiście rozgrzane powietrze – gorąca woda ogrzała powietrze wewnątrz balonika; wraz ze wzrostem temperatury rośnie ciśnienie: rośnie prędkość cząsteczek gazu, te uderzają o ścianki zbiornika i (jeśli to jest możliwe – guma jest bardzo elastyczna) powiększają jego objętość.

Rys. 1. Balonik w a) i b) zanurzony w bardzo gorącej wodzie, c) po wyjęciu z gorącej wody.

Swego czasu tego rodzaju przemiana gazowa, przy zmieniającej się temperaturze, a pod stałym (w przybliżeniu) ciśnieniu, nazywano przemianą izobaryczną, a jej prawo opisywano jako

V/T= const

gdzie V jest objętością a T temperaturą (w Kelvinach). To prawo określa się też nazwiskami Charlesa i Gay-Lussaca (dwóch francuskich uczonych z XVII wieku). Ładną animację zobaczysz na stronie NASA (zobacz: https://www.grc.nasa.gov/www/k-12/airplane/glussac.html)

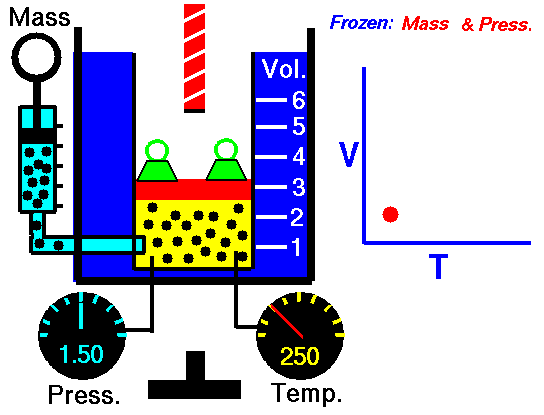
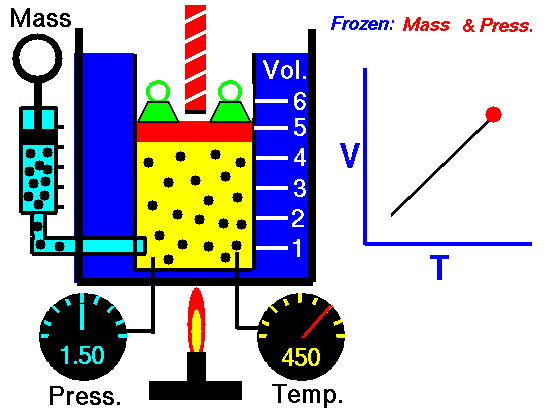
Rys. 2. Animacja NASA (Prawo Charlesa i Gay-Lussac’a).

Wykresem zależności objętości od temperatury (w skali absolutnej, dawniej zwaną skalą gazową) jest linia prosta – zależności wprost proporcjonalnej. W naszym doświadczeniu zmiana temperatury na skali gazowej nie jest wielka – od około 10ºC, gdy woda jest zimna (283 K) do około 90ºC (gdy woda w garnku jest bliska wrzenia). Na wykresie V(T) jest to niewielki odcinek.

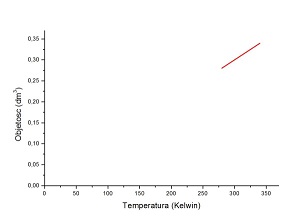
Rys. 3. Zmiana temperatury w butelce zamkniętej balonikiem nie jest duża w skali absolutnej (niecałe 100 K, wobec 300 K temperatury pokojowej). Z tego tez powodu, balonik „nadmuchuje się” niewiele.