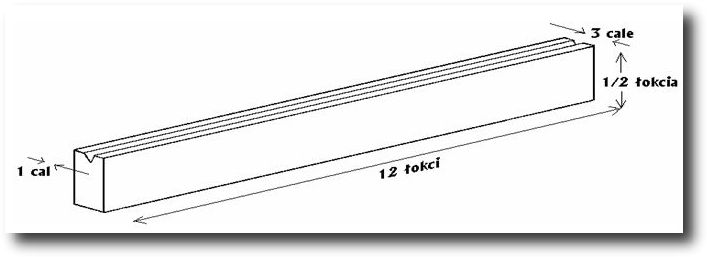
Występują: Galileusz (G), Jego uczennica Ania (A) oraz Narrator (N).

N: Witam Wszystkich na naszych wspaniałych pokazach.
Przedstawiam Wam Profesora Galileusza, naszego wspaniałego uczonego, który  ponad 400 lat temu odkrył prawo ruchu wahadła, obserwując w katedrze w Pizie wahania rozkołysanego świecznika, odkrył także prawo swobodnego spadania ciał, a także jako jeden z pierwszych zbudował lunetę i zastosował ją do obserwacji astronomicznych.
 
Za chwilę dowiecie się, w jaki sposób Galileusz odkrył prawo spadku swobodnego. Przyjęło się powszechnie uważać, że dokonał tego upuszczając różne przedmioty ze szczytu krzywej wieży w Pizie. W rzeczywistości tak jednak nie było. Jak było naprawdę przedstawi nam to sam Galileusz ze swoją pilną uczennicą Anią.

G: Nazywam się Galileusz (Galileo Galilei). Jestem matematykiem, fizykiem, astronomem i filozofem włoskim, profesorem na uniwersytecie w Pizie i Padwie.
Oczywiście, chętnie Wam pokażę moje słynne doświadczenie z równią pochyłą, ale moja uczennica Ania będzie musiała mi w tym pomóc.

A: Panie Profesorze, bardzo chętnie Panu pomogę!

N: Galileusz chcąc ilościowo zbadać zagadnienie spadku swobodnego posłużył się udoskonaloną przez siebie równią pochyłą o długości 12 łokci i wysokości ½ łokcia. Na jej powierzchni polecił wyciąć półkolisty rowek o głębokości ½ cala, biegnący wzdłuż całej równi i wykleić go pergaminem. Po tak przygotowanym torze toczył on kule wykonane z różnych dostępnych wówczas materiałów, tj. drewna, marmuru i mosiądzu. Zobaczcie zresztą to sami.

G: Puszczam kulkę stalową z punktu początkowego równi, co powoduje jej ruch w dół.

A: (Łapie kulkę u dołu równi) Mam ją!

N: Do pomiaru czasu trwania ruchu kul Galileusz zbudował przemyślny zegar wodny, którego dokładność zadziwia jeszcze i dziś, a wynosi ona 0,1 sekundy. Dodatkowo zmieniając kąt nachylenia równi mógł zmieniać czas trwania eksperymentu. Zobaczcie, jak można „zważyć czas”.

G: (Odkręca kranik z wodą i puszcza kulkę drugi raz) Teraz zmierzę dokładnie czas ruchu kulki ważąc wodę zgromadzoną w naczyniu za pomocą wagi szalkowej.

N: Aby otrzymać zależność pomiędzy drogą i czasem dla ruchu jednostajnie przyspieszonego Galileusz wykonuje po 1 pomiarze ruchu kul wzdłuż całej długości równi, a następnie w ¾, ½ i ¼ jej długości.

G: (Puszcza kulkę z góry równi, odkręca kranik z wodą i mierzy czas ruchu kulki.)
Aniu zapisz wynik na tablicy.

A: Zapisuje wynik na tablicy.
Dla L      m = 162 g

G: (Puszcza kulkę z ¾ długości równi, odkręca kranik z wodą i mierzy czas ruchu kulki.)
Aniu zapisz kolejny pomiar.

A: Zapisuje wynik na tablicy w kolejnym wierszu.
Dla ¾ L      m = 139 g
 
G: (Puszcza kulkę z ½ długości równi, odkręca kranik z wodą i mierzy czas ruchu kulki.)
Aniu zapisz proszę, masa wody wynosi:

A: Zapisuje wynik następnym wierszu.
Dla 1/2 L      m = 110 g

G: (Puszcza kulkę z 1/4 długości równi, odkręca kranik z wodą i mierzy czas ruchu kulki.)
Masa wody dla ¼ długości równi wynosi:

A: Zapisuje na tablicy w kolejnym wierszu:
Dla ¼ L      m = 77 g

G: Jeśli teraz wykonam odpowiednie obliczenia to mogę stwierdzić, że: stosunek odpowiednich odcinków drogi równy jest stosunkowi kwadratów odpowiadających im mas wody (kwadratów odpowiadających im czasów ruchu kulek), czyli:

(zapisuje na tablicy)       
oraz

Stąd wniosek, że czas spadania lub toczenia się kulek nie zależy od masy.

Ależ jestem szczęśliwy, odkryłem właśnie prawo spadku swobodnego!

A: Gratuluję Panu Panie Profesorze.

Uwaga: na rysunku poniżej pokazany jest schemat historycznej równi (rynny) Galileusza.