Abstrakt

W artykule opisujemy trzy zagadnienia optyki geometrycznej, zazwyczaj pomijane w na­uczaniu fizyki:

1) zależność ogniskowej od ośrodka, w którym znajduje się soczewka
2) sferyczne powierzchnie załamujące (półsoczewki)
3) soczewki w formie pełnej kuli.

Spis przykładów rachunkowych: Oko płetwonurka Szklana kula Mucha w bursztynie Guzik w pralce Dioptria, program GWBasic

Spis galerii fotografii: Szklane kule z bąbelkami powietrza Żelatynowe świece Szklane kule Szklanka z wodą Dioptria dla dorosłych Butelka wody mineralnej Dioptria z pingwinem WC globus

Spis filmów: Tańczące pingwiny Trzy pingwiny Szklanka i nożyczki Szklanka i pingwin

1. Grube jest piękne, albo przynajmniej było na obrazach Rubensa (1577–1640). Od czasów traktatu pt. „Optyka” Izaaka Newtona (1704) grube są w niełasce, a panują niepodzielnie soczewki cienkie, które opisuje równanie

1/f=1/p+1/q                                                         (1a)

gdzie f zależy od promieni krzywizny soczewek w sposób następuj±cy

1/f=(n–1)(1/R₁ + 1/R₂)                                           (1b)

a n jest współczynnikiem refrakcji, czyli załamania, materiału soczewki.

(Dla przypomnienia, jeśli soczewka jest wklęsła, to promienie krzywizny uważa się za ujemne; w konsekwencji, jeśli q jest ujemne, to obraz jest pozorny – powstaje po tej samej stronie co przedmiot.)

Wszystko co nie spełnia równanie (1) nazywane jest aberracją, czyli zboczeniem. Okazuje się, że zboczeń jest więcej niż przypadków prawowitych.

2. Na ogół milcząco zakłada się, że przed i za soczewką znajduje się powietrze (o współczynniku załamania w przybliżeniu n = 1). Jeśli jest inaczej, jak np. w przypadku bąbelków wody w oleju lub innych dwóch różnych cieczy, fot. 1, „wypukły” bąbelek staje się soczewką rozpraszającą. Podobnie jest w przypadku straganu ze wszystkimi rozmiarami baterii, jak na fot. 2. (Młodzież nie pamięta, ale jeszcze 20 lat temu zdobycie np. baterii paluszków było nie lada wyczynem han­dlowym; nasz projekt rozwiązuje ten problem).

Pełne równanie soczewki, uwzględniające trzy różne ośrodki: n₁ w którym znajduje się obiekt, n₂ materiału soczewki i n₃ materiału, w którym powstaje obraz, nie jest wcale takie proste:

n₁/p + n₃/q = (n₂ – n₃)/R₂ + (n₂ – n₁)/R₁                          (2)

Fot. 1. Kaczki w szklanej popielniczce: jest to przykład dwóch cieczy niemieszaj±cych się. Ciecz niebieska, mimo że cięższa, ma niższy współczynnik załamania niż ciecz bezbarwna. Potrząsanie popielniczką wytwarza bąbelki jednej cieczy w drugiej (lub bąbelki powietrza), które działają jak soczewki rozpraszające. Taki sam efekt można uzyskać nalewając do słoika 0,5–1 cm3 oleju, a następnie gwałtownie zamieszać, dla utworzenia bąbelków po­wietrza; jeszcze lepiej zamieszać olej z wodą

Fot. 2. Stragan z bateriami wszystkich rozmiarów. Baterie są oczywiście jednego, jedynego rodzaju, jak niegdyś w PRL, a jedynie woda się znajduje raz w szklance, raz w akwarium (a czasem w głowie)

Ogniskowa (tzn. q dla warunku p = ∞) wynosi q = n₃[R/(2n₂ – n₃ – n₁)] gdzie za­łożyliśmy dla uproszczenia R₁ = R₂. Ponieważ wewnątrz ludzkiego oka n₃ odpo­wiada „ciału szklistemu”, czyli praktycznie wodzie, a współczynnik załamania soczewki oka nie jest wiele większy od 1,0, to pływak bez okularów do nurkowa­nia widzi wszystko rozmazane, tak jak dalekowidz w – „brylach jak lunety” (rozwiązanie zadania).

3. W równaniach (1) i (2) nadal pozostają ukryte założenia: 1) że promienie bie­gną blisko osi soczewki (co jest równoważne założeniu o dużym promieniu krzy­wizny soczewki) i 2) że soczewka jest cienka.

        Jeśli soczewka nie jest cienka, to promienie równoległe, biegnące z nieskoń­czonej odległości, ale leżące w różnej odległości od osi optycznej, wcale nie sku­piają się w jednym punkcie. Taką aberrację nazywamy sferyczną, bo poniekąd jest spowodowana kulistą formą soczewki – grubszą nieco w środku. Jest to jed­nakże tautologia, bo soczewki są sferyczne (tak je łatwiej szlifować). W przy­padku luster – aby promienie skupiały się w jednym punkcie, forma zwierciadła powinna być paraboliczna, co z kolei ogranicza ich kątowy zakres obserwacji.

4. Z tej samej sferycznej formy soczewki cienkiej wynika, że jeśli obiekt nie znaj­duje się na osi optycznej, to jego obraz jest zniekształcony – punktowe źródło światła zamienia się w przecinek (aberracja nosi nazwę „komy”). I jest jeszcze aberracja chromatyczna – wynikająca z zależności współczynnika załamania od długości fali światła. Tę aberrację usuwa się składając dwa gatunki szkła, które w podręcznikach nazywa się „crown” – szkło krzemowo-potasowe (n=1,52) oraz „flint” (n=1,65) – o dużej zawartości tlenku ołowiu, otrzymywane z domieszką specyficznego margla. Nazwy pochodzą jeszcze z pozwolenia na produkcję, wydanego przez króla Anglii w 1676 roku dla niejakiego George'a Ravenscrofta, który podobno wywiózł sekrety produkcji szkła optycznego z Wenecji.

5. Jeśli soczewka jest gruba, to wcale nie jest powiedziane, że promienie biegnące z nieskończoności skupią się w tej samej odległości od „środka” soczewki. Co zresztą jest „środkiem” soczewki? W tym przypadku każdą płaszczyznę rozgrani­czającą powietrze/szkło, a następnie szkło/powietrze należy rozważać oddzielnie, jako tzw. dioptrię, czyli półsoczewkę. Czytelnikom Fizyki w Szkole równanie dioptrii nie powinno być obce, bo zostało ostatnio „przemycone” z zadaniami z Olimpiady Fizycznej [2]. A jest ono np. w programie włoskich liceów.

n₁/p + n₂/q = (n₂ – n₁)/R                                          (3a)

gdzie podobnie jak w równaniu (1) zakłada się, że przedmiot leży na lewo od granicy rozdziału dwóch ośrodków, natomiast promień krzywizny R uważa się za dodatni, jeśli środek krzywizny leży na prawo od granicy ośrodków, zaś ujemne q oznacza, że obraz powstaje po tej samej stronie co przedmiot (czyli po lewej).

Powiększenie dioptrii wyraża się wzorem

I = n₁q/n₂p = (q – R)/(p + R);                                    (3b)

gdzie  ujemny znak I oznacza obraz prosty (nieodwrócony). 

6. Raz poznawszy równanie półsoczewki, jesteśmy w stanie wyjaśnić rachunkowo wielkość bąbli powietrza w szklanej lub żelatynowej kuli (lub np. pachnących, żelatynowych świecach. Dla przykładu, bą­bel w głębi kuli (np. 15 cm od „przedniej” powierzchni) o średnicy 20 cm (w tym przypadku należy przyjąć promień R = –10 cm w równaniu dioptrii) będzie wy­dawał się 1,6 razy większy, jeśli pływa w wodzie (n = 1,33) i 2 razy większy, jeśli jest zatopiony w szkle (n = 1,5). Jeśli natomiast umieścimy go bliżej, np. 5 cm od przedniej ścianki, to powiększenie w szkle zmniejszy się do 1,2 raza. W granicz­nym przypadku, przedmiot na końcu kuli jest powiększony n/(n – 2) razy, czyli dla szkła 3 razy, niezależnie promienia, zob. fot. 3.

Fot. 3. Kula z weneckiego szkła – przykład półsoczewki. Owalny kwiatek w głębi kuli wydaje się 3 razy większy niż ten z przodu. Deformacje kwiatków na brzegach kuli są dowodem, że równanie półsoczewki korzysta z tych samych założeń, co równanie soczewki cienkiej: promieni przyosiowych. Jeśli promienie nie są przyosiowe, to równania (1)–(3) się nie stosują.	Fot. 4. Nierównomierne powiększenie obiektu w kuli, w za­leżności od jego położenia, czyni z krasnala potwora. Etykieta sklepowa leży poza kulą – jej zniekształcenie pokazuje, że optyka grubych soczewek jest dla promieni nieprzyosio­wych – bardzo skomplikowana.

Ponieważ powiększenie zależy od położenia, postacie całkiem proporcjonalne, np. krasnal na fot. 4, stają się w „magicznych” kulach karykaturami.

6a. Dioptria wklęsła daje oczywiście obrazy pomniejszone (promień krzywizny jest dodatni, zob. przykład liczbowy w [1]), jak np. fotelik z pingwinami, fot. 5, czy „Ostatnia Wieczerza”, fot. 6 (z Republiki Ludowej Chin, czegóż nie robi się dla pieniędzy!).

Fot. 5. Zmienny promień krzywizny – raz dodatni raz ujemny, tworzy z fotelika z pingwi­nami obiekt nie mniej zajmujący niż kalejdoskop (zob. też [1]). Tańcz±ce pingwiny Trzy pingwiny	Fot. 6. Chińska „Ostatnia Wieczerza” – wklęsła półsoczewka pomniejsza

7. Gdy już umiemy liczyć półsoczewki, to soczewka gruba jest niczym innym jak złożeniem dwóch półsoczewek: powietrze/szkło + szkło/powietrze. Dla przykładu ogniskowa soczewki o promieniu 10 cm wykonanej ze szkła (n = 1,5) wynosi 5 cm. Natomiast dla soczewki cienkiej, dwuwypukłej, o obu promieniach krzywizny równych 10 cm, ogniskowa jest dwa razy większa, 10 cm.

I tu widać sens używania soczewek cienkich: w soczewce grubej, aby uzyskać obraz powiększony i prosty (jak w lupie), obiekt musi się znajdować bardzo blisko niej. W naszym przykładzie liczbowym, zmieniając odległość obiektu od szklanej kuli z 3 cm na 4 cm powiększenie rośnie z 7,5 na 15 razy^*). W analogicznej so­czewce cienkiej powiększenia zmieniają się mniej, z –4,3 na –6,6 raza dla powyż­szych odległości. Soczewka gruba jest więc obiektem „bliskowidzącym”.

Powiększenie przedmiotu leżącego tuż za kulą (p = 0) wynosi – podobnie jak dla przedmiotu leżącego na „końcu” kuli – n/(n – 2), czyli 3 dla szkła o n = 1,5.

Dla odległości większych od ogniskowej powstające w kuli obrazy są odwró­cone, podobnie jak dla soczewek cienkich, zob. fot. 7.

Fot. 7. Jedna wieża Eiffla jest umieszczona w kuli – kula działa jak półsoczewka. Wieża odwrócona to obraz wieży z kuli sąsiedniej – dwie kule tworzą coś w rodzaju mikroskopu: jedna wytwarza obraz rzeczywisty odwrócony, druga tworzy z niego obraz pozorny	Fot.8. Płytka równoległościenna to też gruba soczewka (złożenie dwóch półsoczewek o promieniach R = ∞). Nie powiększa, a tylko przybliż

 
8. Pierwsze mikroskopy były jednak budowane z soczewek grubych – szklanych kul. Ich konstruktor, Anton van Leeuwenhoek przeszedł do historii jako twórca mikrobiologii, zupełnie przez przypadek. Handlował suknem i przyprawami i któ­regoś dnia postanowił sprawdzić, dlaczego pieprz piecze. Podejrzewał, że nasion­ka mają małe haczyki, którymi przyczepiają się do języka. Rozgniótł więc trochę nasion pieprzu i zalał wodą, aby namiękły. Był jednak zajęty sprawami zawodo­wymi, więc obejrzał pieprz dopiero po paru dniach: roiło się w nich od mikro­bów.

9. Równanie dioptrii pozwala też wyjaśnić, dlaczego ryby w wodzie i pranie w pralce (oglądane przez szklany wziernik) wydają się położone bliżej niż w rze­czywistości. Wystarczy w tym celu promień krzywizny dioptrii przyjąć R = ∞ i w konsekwencji równanie (tzw. dioptrii płaskiej) przyjmuje postać q = –(n₂/n₁)p, a powiększenie wynosi I = –1 (obraz jest pozorny). Efekt „przybliżenia” jest znaczny, jeśli dioptrią jest np. szklany sześcian, uchwyt na notatki, fot. 8.

 I tak np. guzik w pralce w odległości 10 cm od wziernika o grubości 1 cm wydaje się być położony w odległości 8,2 cm, a nie 11 cm. To samo zagadnienie da się rozwiązać analizując bieg promieni załamanych, ale pytanie brzmi wówczas: „Rybak widzi szczupaka pod kątem 50°, pozornie na głębokości 2m; gdzie znajduje się szczupak?”

10. Ciągle jednak nie pozbyliśmy się założenia 1) – promieni przyosiowych (pa­raksjalnych). Jak widać na zdjęciu nr 9, zwykła szklanka staje się skomplikowa­nym urządzeniem optycznym, które trudno przybliżyć jakimś równaniem – z po­mocą przychodzą komputery [3]. Skomplikowane bryły soczewek dostarczają efektów zupełnie niespodziewanych, jak rozdwojenie obrazu na fot. 5.

Fot. 9. Nawet zwykła szklanka pokazuje, jak skomplikowana jest optyka promieni nieprzyosiowych (fot. A. Krzysztofowicz) Szklanka i nożyczki Szklanka i pingwin

Fot. 10. Wałki z pleksiglasu są też grubymi soczewkami – cylindrycznymi. Podobnie jak w przypadku szklanej kuli, obiekty umieszczone tuż za soczewką są powiększane w czyn­nik n/(n – 2), niezależnie od promienia pręta, co widać na zdjęciu "Szklanka do czytania"

Nawiasem mówiąc, i szklanka i wałek plexi są soczewkami cylindrycznymi, a nie sferycznymi. Równanie soczewki cylindrycznej jest takie same jak sferycznej, tylko że w jednym wymiarze: soczewka z bliska powiększa, zob. fot. 10, z daleka odwraca, fot. 11.

Fot. 11. Akwarium z rybkami w witrynie sklepu w Antony (Paryż) działa jak soczewka cylindryczna – odwraca w jednym wymiarze napis z dziecięcej torebki

Rys. 12. Soczewka mikroskopu elektronowego składająca się z dwóch współosiowych cylindrów: linie przerywane pokazują rozkład potencjału elektrycznego (są to linie ekwi­potencjalne) – pole elektryczne jest do tych linii prostopadłe. Elektron jest odchylany przez pole, jak poziomo lec±cy kamień przez pole grawitacyjne Ziemi. Ten przykład (energia elektronów 200 eV, U1 = +100V, U2 = +30V) to soczewka wytwarzająca równoległą wiązkę elektronów (obliczenia D. Pliszka).

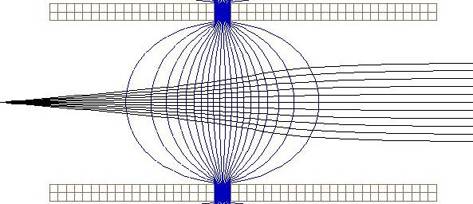
11. Bez znajomości soczewek grubych nie można zrozumieć, jak działa mikro­skop elektronowy. Soczewki dla elektronów – dwa cylindry, do których przyło­żone zostają różne potencjały, to właśnie grube, cebulowate struktury. Elektron jest odchylany przez pole elektryczne w całym obszarze wewnątrz takiej cebuli. Do symulacji jego toru też używa się programów komputerowych [4] (fot. 12).

12. A przypadek van Leeuwenhoeka jest typowym przykładem pożytków płyną­cych z twórczej swobody niesubordynacji naukowców: zamiast koncentrować się na zaplanowanych badaniach, zajął się mikrobiologią. W rezultacie wynik, że mamy dziś DNA, mutacje, i klony. A haczyki w pieprzu nadal czekają na swego odkrywcę!

Literatura:

Opiekun Strony: Krzysztof Służewski