Mucha w bursztynie

Obliczmy powiększenie przedmiotu położonego w kuli o promieniu R w odległości p od jej powierzchni. Przypominamy, że obowiązuje zasada promieni przyosiowych – tzn. “powierzchnia” kuli może być przybliżona przez odcinek styczny – jak czerwona linia na poniższym rysunku. Ponieważ środek krzywizny powierzchni granicznej znajduje się na lewo od tej powierzchni, przypisujemy promieniowi krzywizny znak ujemny R<0.

W podanym w artykule przykładzie liczbowym mamy:
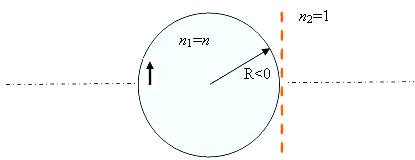
p = 15 cm
R = -10 cm
Zakładamy  n₁ = 1,33 = n (woda)
n₂ = 1  (powietrze)


Równanie dioptrii ma postać

 n₁/p + n₂/q = (n₂-n₁)/R

Dla  n₁ = n  i  n₂ = 1 równanie to przyjmuje postać    

n/p + 1/q = (1-n)/R

skąd otrzymujemy  1/q = (1-n)/R - n/p

i       q = 1 / [(1-n)/R + n/p]

Podstawiając wartości liczbowe otrzymujemy q = 1 / [(1 - 1,33) / (-10) - 1,33 / 15] ≈ -18,0 cm
(znak minus oznacza, że obraz powstaje w lewej strony powierczhni jranicznej, czyli jest pozorny).

Powiększenie wynosi I = n₁q/n₂p = -1,33∙18 / 15 = -1,6
(znak minus oznacza, że obraz jest nieodwrócony).

W przypadku szklanej kuli n = 1.5, obraz powstaje w odelgłości q = -20 cm  powiększenie wynosi I = -2 (obraz jest powiększony i nieodwrócony).
Jak widać z przykładu, obliczenia dla dioptrii, czyli półsoczewki są stosunkowo proste. Trudniej jest natomiast zrobić rysunek. Dwa ogniska dioptrii, przednie i tylne znajdują się w różnych odległościah od powierzchni granicznej – trzeba je szczegółowo wyliczyć. Wiadomo jedynie, że promień wychodzący z przedmiotu załamuje się na powierzchni granicznej zgodnie z prawem Snella -
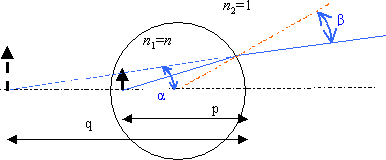
sinα/sinβ = n₂/n₁ .

W naszym przypadku kąta padania (α, w kuli) jest mniejszy od kąta załamania (β, w powietrzu), jak na rysunku powyżej.