Due sfere rigide sono sospese su due cordicelle distinte. Con un movimento ritmico si puo portarle ad urti ripetuti. Ciascuna delle sfere si muoverà sul suo semicerchio rimbalzando sulla "compagna" nelle posizioni più alta e più bassa. Se non mettessimo continuamente in moto le sfere, esse smetterebbero subito di scontrarsi. Non esistono urti perfettamente elastici e in ciascun urto le sfere perdono un po' di energia, se non altro per fare rumore.
Le sfere hanno massa identica, si scontrano centralmente con velocità opposte in verso, ma identiche. Rimbalzano quindi in direzioni opposte, sempre con velocità identiche. Se una delle due sfere è a riposo, allora dopo l'urto si allontanano formando un angolo retto (oppure una di esse si ferma, se l'urto è centrale, come nel pendolo di Newton).
Ma, in generale, questa non è affatto una questione semplice.
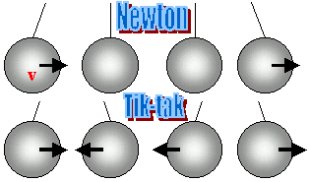
Un ritmico movimento della mano fornisce alle sfere tanta energia, quanta ne hanno persa nell'urto - esse quindi non accelerano, né rallentano.
D'altro canto, osservando attentamente il modo con cui si provocano gli urti, si arriva alla conclusione che il movimento della mano deve farsi nel piano delle traiettorie dei centri di massa delle sfere. Questo significa che gli urti devono essere centrali, se vogliamo che il "riki-tiki" riesca perfettamente.
Il riki-tiki èuna sorta di pendolo di Newton, composto di due sfere. A differenza del pendolo di Newton, entrambe le sfere si muovono. Indichiamo con v e -v le loro velocitàiniziali e con V1 i V2 le loro velocitàdopo l'urto.
L'equazione di conservazione della quantitàdi moto assume la forma:
mv - mv = mV1 + mV2 da cui segue V1 = - V2
e quella della conservazione dell'energia
½mv2 + ½mv2 = ½mV12 + ½mV22
da cui, dopo aver messo i valori assoluti ad entrambi i membri della prima equazione, otteniamo |V1| = |V2| = |v|. Questo risultato ci dice soltanto a quanto ammontano i valori assoluti delle velocitàe non quale delle velocitàa, V1 o V2