W rozważaniach
bardziej szczegółowych nie chodzi nam tym razem o tęczę
wtórną, ale o tzw. tęcze wielokrotne składające się z
szeregu mniej widocznych łuków znajdujących się wewnątrz tęczy
właściwej, a bardzo rzadko również i na zewnątrz łuku tęczy
wtórnej. Niekiedy można też zauważyć wyraźną różnicę jasności
nieba wewnątrz i na zewnątrz tęczy, podobnie jak na poniższym
zdjęciu:

Fot. 1. Zdjęcie ukazuje różnicę jasności nieba wewnątrz i na zewnątrz tęczy oraz tęcze wielokrotne (wewnątrz tęczy właściwej).
Źródło: https://www.europhysicsnews.org/articles/epn/pdf/2006/01/epn06103.pdf
Tęcze wielokrotne
Tęcze wielokrotne są najlepiej widoczne, gdy krople są
niewielkie i jednakowej wielkości. Sam fakt ich występowania
był historycznie pierwszą wskazówką, że światło ma naturę
falową, a pierwsze wyjaśnienie tego zjawiska zostało
zaproponowane przez Thomasa
Younga w 1804 roku.
Tęcze takie tworzą się w wyniku interferencji promieni światła załamanych pod mniejszym kątem, bo padły bliżej środka kropli, oraz promieni z maksimum, które uległy dyfrakcji (teoria Airy’ego). Gdy te dwa promienie po wyjściu z kropli będą w fazie fali, wzajemnie wzmocnią się (powstaną jaśniejsze kręgi), gdy fale będą miały przeciwne fazy, wytłumią się (kręgi ciemniejsze). Warunki fazowe zależą od długości fali, dlatego kręgi są kolorowe.
Przyjrzyjmy
się, jak wygląda załamanie na powierzchni kropli wody, w
szczególności zwróćmy uwagę na fakt, że front fali przestaje
być prosty:

Rys. 1. Przejście promienia i frontu fali przez kropelkę wody. Wg https://www.ams.org/samplings/feature-column/fcarc-rainbows
Pojawia się tu matematyczny problem: jak opisać rozchodzenie się fali o froncie w kształcie litery S?
Jest to szczególny przypadek zasady Huyghensa, mówiącej, iż każdy punkt ośrodka, do którego dotarło czoło fali można uważać za źródło nowej fali kulistej. Jeśli dobierzemy układ współrzędnych tak, by oś symetrii pokrywała się z osią X, krzywą o kształcie litery S możemy przybliżyć za pomocą funkcji y = kx3. Współczynnik k możemy określić jako k = c/R2 , gdzie c jest stałą bezwymiarową, a R promieniem kropli.
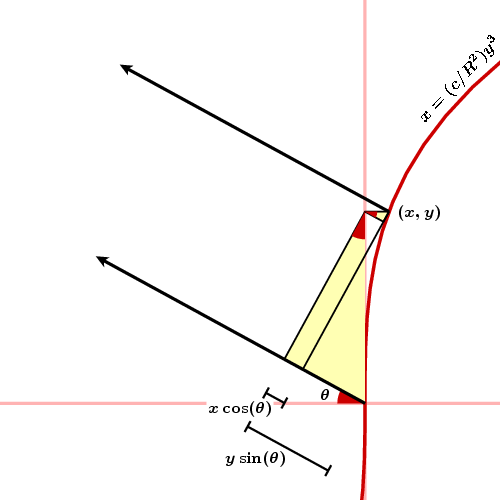
Rys. 2. Pomocniczy rysunek do określenia funkcji Airy’ego. (wg https://www.ams.org/samplings/feature-column/fcarc-rainbows)
Amplituda
obserwowana jest sumą poszczególnych wkładów – z
matematycznego punktu widzenia całką
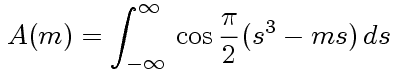
Jej graficzne rozwiązanie pokazuje poniższy rysunek:

Rys. 3. Natężenie światła o różnej barwie (niebieskiej, zielonej i czerwonej) rozproszonego przez kropelki wody o promieniu (a) 0,3 mm i (b) 0,05 mm. Ilustracja pochodzi z artykułu Davies, Wannell, Inglesfield „The rainbow” opublikowanego na łamach Europhysicsnews 1/2006 (patrz też https://www.europhysicsnews.org/articles/epn/pdf/2006/01/epn06103.pdf)
Treść i układ
html: K. Rochowicz
