
艢migus-dyngus
Taka sama ilo艣膰 wody, jaka jest przesuwana za pomoc膮 t艂oka, musi si臋 jednocze艣nie (w danej chwili) przecisn膮膰 przez cienki otw贸r wylotowy. O tym m贸wi prawo zachowania masy, kt贸re prowadzi do r贸wnania ci膮g艂o艣ci: iloczyn g臋sto艣ci wody r, pola powierzchni t艂oka S1 i pr臋dko艣ci wody v1 w komorze z t艂okiem (jest to masa przep艂ywaj膮cej wody w jednostce czasu) musi by膰 r贸wny iloczynowi r贸wnie偶 g臋sto艣ci wody oraz pola powierzchni przekroju otworu wyj艣ciowego S2 i pr臋dko艣ci v2 w tym偶e otworku:
Jak wida膰, pr臋dko艣膰 wylotowa wody jest proporcjonalna do pr臋dko艣ci przesuwu t艂oka i wi臋ksza od niej o stosunek p贸l powierzchni t艂oka do otworu wylotowego.
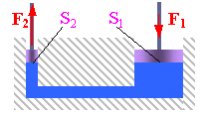
Analogicznie jest z si艂ami dzia艂aj膮cymi w prasie hydraulicznej (patrz: rysunek). Dzia艂aj膮c na t艂ok o powierzchni S1 si艂膮 F1, na drugi t艂ok b臋dzie dzia艂a膰 si艂a wi臋ksza o stosunek powierzchni p贸艂 t艂ok贸w, r贸wna
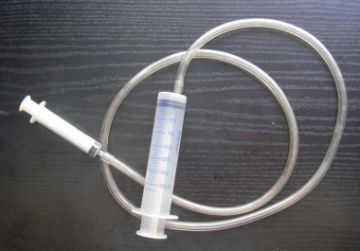
Mo偶esz 艂atwo zrobi膰 tak膮 pras臋 z dw贸ch strzykawek lekarskich o r贸偶nych przekrojach, po艂膮czonych w臋偶ykiem (i wype艂nionych wod膮! Powietrze jest zbyt 艣ci艣liwe, aby prasa dobrze dzia艂a艂a.)
