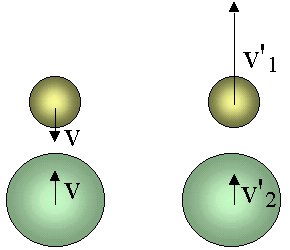
Herunterfallende Bälle

Der leichtere Ball würde niemals höher schießen, würde er allein auf den (unbewegten) Boden prallen.

WIn Wirklichkeit haben wir es mit einem (unscheinbaren) Zusammenstoß der beiden Bälle zu tun. Der rote Ball prallt früher vom Boden ab und verändert seine Geschwindigkeitsrichtung, während der Geschwindigkeitsvektor des orangen Balls immer noch nach unten gerichtet ist. Als Folge des elastischen Stoßes wird der Impuls des schwereren Balles an den leichteren übertragen und damit prallt der leichtere Ball auf eine viel größere Höhe ab.

Lasst uns dies genauer erklären. Sei die Masse des leichteren Balls mund die des schwereren M und nehmen wir an, dass sie aus der Höhe h, losgelassen wurden, dann sagt uns der Energieerhaltungssatz, dass im Moment des Zusammenstoßes die Geschwindigkeit des kleineren Balls -v und die des größeren v (ist (also mit entgegen gesetzten Vorzeichen). Der Energieerhaltungssatz liefert unter Annahme eines elastischen Stoßes:

Der Impulserhaltungssatz liefert:

Die Geschwindigkeiten nach dem Stoß betragen somit:

für den leichteren und

für den schwereren Ball.

Unter der Annahme, dass m viel kleiner ist als M kann man die obigen Werte nähern:

Also wird der kleinere Ball nach Beachtung, dass seine kinetische Energie in potenzielle umgewandelt wird, neunmal höher springen als der schwere.

Das Ergebnis v₁' = 3v und v₂' = v scheint allen Gesetzen zu widersprechen: Der schwerere Ball hat seine Geschwindigkeit beibehalten und der leichtere seine "aus dem Nichts" verdreifacht. Dieser scheinbare Widerspruch folgt aus der Näherung M >> m; bei einem Zusammenstoß eines Basketballs mit einem Tischtennisball wäre dies so. Weil die Ballmassen nicht ganz so verschieden sind, beobachten wir genau dass, was das Experiment zeigt: Der leichtere Ball fliegt höher, um ein Vielfaches höher als die Ausgangshöhe und der schwerere etwas niedriger.