
Pistolet ŕ eau
La męme quantité d'eau que l'on déplace ŕ l'aide du piston, doit au męme instant passer ŕ travers l'étroite ouverture de sortie. De cela traite le principe de conservation de la masse, qui mčne a l'équation de continuité : le produit de la densité de l'eau r, de la surface du piston S1 et de la vitesse de l'eau v1 dans le compartiment avec piston (c'est une masse d'eau qui passe dans l'unité de temps) doit ętre égal au produit de la męme densité, de la surface de la section de l'ouverture de sortie S2 et de la vitesse de l'eau v2 dans ladite ouverture.
Comme l'on voit, la vitesse d'éjection de l'eau est proportionnelle ŕ la vitesse d'avancement du piston, et plus grande d'elle d'un facteur égale au rapport entre les sections.
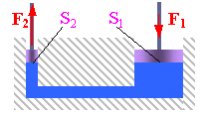
De męme ça se passe avec les forces agissant dans une presse hydraulique (voir dessin). En actionnant le piston de surface S1 par une force F1, sur l'autre piston va agir une force plus grande du rapport des sections des pistons, égale ŕ
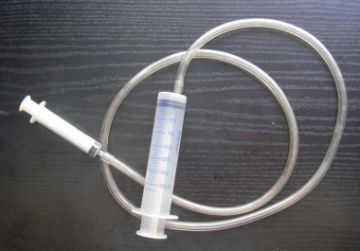
On peut réaliser aisément une telle presse ŕ l'aide de deux syringues de différentes sections, reliées par un tuyau (et pleines d'eau! L'air est trop compressible pour que la presse fonctionne bien).
