Riki tiki
Le mouvement rythmique de la main fournit aux sphčres autant d'énergie qu'elles ont perdu pendant le choc - elles n'accélčrent pas et ne ralentissent pas.
D'autre côté, on observant attentivement la façon de laquelle les chocs se passent, on arrive ŕ la conclusion que le mouvement de la main doit avenir dans le plan des trajectoires des centres de gravité des sphčres. Cela signifie que les chocs doivent ętre centraux, si l'on veut que le " riki-tiki " réussisse parfaitement.
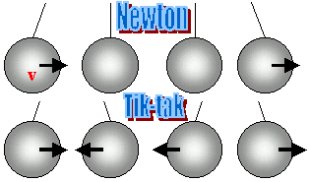
Le riki-tiki est une sorte de pendule de Newton, composé de deux sphčres. Ŕ différence du pendule de Newton, les deux sphčres bougent. Indiquons par v et -v .v et -vleur vitesses initiales, et par V1 i V2leur vitesses aprčs le choc.
L'équation de conservation de la quantité de mouvement prend la forme :
mv - mv = mV1 + mV2 d'oů V1 = - V2
et celle de la conservation de l'énergie
˝mv2 + ˝mv2 = ˝mV12 + ˝mV22
d'oů, en prenant en compte la premičre équation, on obtient |V1| = |V2| = |v|. Ce résultat nous dit seulement combien sont les valeurs absolues des vitesses, et ne pas quelle vitesse V1 ou V2 , est positive et quelle négative. Donc en effet on ne sait pas, quelle sphčre est allée vers la droite et quelle vers la gauche (et si le choc a effectivement eu lieu…).