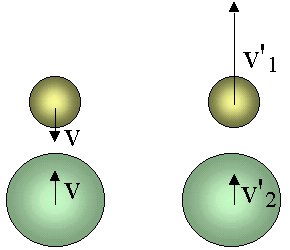
Palline in caduta libera

La pallina più leggera non andràpiù in alto, se rimbalzeràdal pavimento (immobile).

In realtàa, abbiamo a che fare con un urto (nascosto) tra le due palline. La pallina rossa rimbalza da terra prima ed inverte il verso della velocitàa, mentre il vettore velocitàdella pallina arancione èancora orientato verso il basso in quel momento. Per effetto di un urto elastico, la quantitàdi moto della pallina più pesante viene comunicata alla pallina più leggera e, di conseguenza, la pallina più leggera rimbalza ad un'altezza molto maggiore.

Spieghiamolo più precisamente. Assumendo che la massa della pallina più leggera sia m e la massa di quella più pesante M ed assumendo che siano state lasciate da un'altezza h, dal principio di conservazione dell'energia otteniamo che, nel momento dell'urto, la pallina più piccola ha velocità-v mentre quella più grande velocità v (cioèdi verso opposto). Applicando il principio di conservazione dell'energia (assumiamo che l'urto sia elastico):

e quello della conservazione della quantitàdi moto

i valori delle velocitàdopo l'urto sono

per la pallina più leggera e

per quella più pesante.

Assumendo ora che m molto più piccola di M si possono approssimare i valori sopra con

cioe, dopo aver messo i valori assoluti ad entrambi i membri, che l'energia cinetica viene convertita in energia potenziale; la pallina più leggera rimbalzeràad un'altezza nove volte più alta di quella più pesante.

I risultati v₁' = 3v e v₂' = v sembrano smentire le leggi di conservazione: la pallina più pesante mantiene la sua velocitàa, mentre quella più leggera la triplica "dal nulla". Questo paradosso apparente deriva infatti dall'approssimazioneM >> m; nell'urto di un pallone da basket con una pallina da ping-pong accadrebbe effettivamente cosi. Ma poiché le masse delle palline non sono poi cosi fortemente differenti, osserviamo proprio cio che mostra l'esperienza: la pallina leggera rimbalza più in alto dell'altezza iniziale, mentre quella pesante rimbalza un po' più in basso.