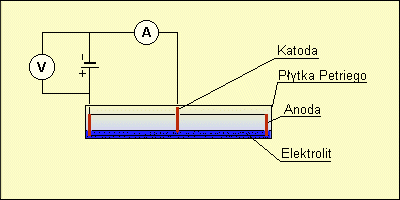
 Schemat układu do elektrolizy
Schemat układu do elektrolizy
Fraktale
W celu otrzymania kryształu dendrytycznego podczas elektrolizy należy w płytce Petriego umieścić elektrolit tak, aby pokrywał dno. Zazwyczaj wystarcza warstwa ok. 1-2 mm grubości. W tejże płytce należy umieścić również elektrodę w kształcie okręgu lub walca o średnicy zewnętrznej niewiele mniejszej od wewnętrznej średnicy naczynia. Wcześniej należy płytkę Petriego odtłuścić, umyć bieżącą woda, przepłukać dokładnie wodą destylowaną i wysuszyć. Podobnie należy postąpić z anodą i katodą: przed przepłukaniem w wodzie można miejsca styku elektrod z elektrolitem przetrzeć papierem ściernym. Do środka należy nalać elektrolitu o stężeniu około 5 %. Jeżeli elektrolitem jest np. siarczan miedzi to anodę najlepiej dobrać miedzianą. Nie należy wlewać zbyt dużej ilości elektrolitu, bowiem w początkowej fazie narastania kryształu będzie on rósł trójwymiarowo. Następnie przykładamy elektrodę centralną symetrycznie, tj. w środku okręgu. Katoda powinna leciutko wchodzić pod powierzchnię elektrolitu. Powinno się przy tym dokładnie zadbać, by całe naczynie z elektrolitem było ustawione dokładnie poziomo. Po ustawieniu zestawu, należy podłączyć do zasilacza wg schematu jak na rysunku poniżej i obserwować proces osadzania elektrolitycznego kryształu.
 Schemat układu do elektrolizy
Schemat układu do elektrolizy
Narastanie kryształu wygląda tak:
Twórca teorii fraktali Benoit Mandelbrot w swojej książce "Fractal Geometry of Nature" [1] podaje wiele przykładów konstrukcji fraktalnych. Matematycy znali wiele konstrukcji trudnych do opisania, jednak prostych do wyobrażenia i wytworzenia. Brakowało spójnej teorii opisującej wszystkie fraktale. Potrzebna ona była nie tylko matematykom, ale głównie naukom przyrodniczym i technicznym. W przyrodzie obiekty fraktalne występowały bardzo pospolicie choćby liście, naczynia krwionośne, łańcuchy górskie, przekroje skał, chmury itp.
B. Mandelbrot, twierdził, ze fraktalem jest wszystko, natomiast figury typu prostokąt, koło, trójkąt są sztucznie wymyślone przez ludzi w celu uproszczenia opisu otaczającego nas świata. Twierdził on bowiem, że figury takie nie mają odpowiedników w rzeczywistości. Gdy popatrzymy na drzewa, chmury, linie górskich szczytów wydaje się ze Mandelbrot miał sporo racji. Rzeczywiście nie ma tam właściwie żadnych figur regularnych. Wszystko jest wystrzępione, fragmentami do siebie podobne.
Mandelbrot w swej pracy "Fractal Geometry of Nature" podaje trzy główne własności fraktali:Ostatecznie fraktal od łacińskiego słowa fractus- 'złamany' to figura geometryczna o złożonej strukturze, nie będąca krzywą, powierzchnią, ani bryłą w znaczeniu geometrii klasycznej, mająca wymiar ułamkowy.
Przy opisywaniu konstrukcji fraktali daje się zauważyć, że są one takie same w każdym swoim kawałku i w każdej skali. Tę cechę nazywa się często samopodobieństwem. B.Mandelbrot do pełniejszego opisu teoretycznego fraktali musiał odpowiednio zmodyfikować topologiczne pojęcie wymiaru , ponieważ klasyczne pojęcie wymiaru nie było zbyt dokładne. Dla przykładu krzywa Kocha to już nie jednowymiarowa linia, ale jeszcze nie dwuwymiarowa powierzchnia.
Wielka popularność fraktali w ostatnich latach wynika m.in. z tego, że do ich konstrukcji można wykorzystywać komputery. Trudno wszak sobie wyobrazić wykonanie wielu tysięcy obliczeń i rysunków ręcznie. Powstało wiele programów do generowania fraktali. Wykorzystuje się je do generowania krajobrazów, roślin, organizmów potrzebnych w dziedzinie filmów, sztuki, nauk przyrodniczych, gier komputerowych, czy w ostatnio do zapisu obrazów przewyższających swoją rozdzielczością i długością plików znane formaty grafiki bitmapowej czy wektorowej. Najłatwiej otrzymywać fraktale na komputerach ze względu na wspólne cechy komputerów i fraktali. Przepis na wytworzenie fraktala jest w sumie bardzo prosty, a jedyny kłopot to konieczność wykorzystania dużej liczby iteracji. W praktyce ta liczba zamyka się w kilkudziesięciu tysiącach powtórzeń. Związane jest to z możliwościami pamięci komputerów i rozdzielczością ekranów monitorów czy drukarek. Tworzenie programów tworzących kolorowe fraktale stało się punktem honoru każdego programisty. W dniu dzisiejszym mamy dostęp do wielu pomysłowych programów tworzących fraktale.
Matematykom nie wystarczyła znajomość prostych reguł tworzenia poszczególnych fraktali i opisywanie ich za pomocą wymiarów, chcieli oni znać własności tych konstrukcji. Bardzo szybko okazało się, że w sposób prosty i pełny można matematycznie opisać własności wszystkich znanych fraktali. Był to początek bardzo ciekawej teorii geometrycznej. Najistotniejsze w tej teorii było spostrzeżenie, że fraktale otrzymuje się za pomocą wielokrotnego stosowania przekształceń afinicznych wyjściowego obiektu. Jedną z podstaw teorii fraktali jest iteracja ;.
"Iteracja to ponowne, powtórne, kolejne zastosowanie przepisu do poprzedniego wyniku, Iterowanie to ... powtarzanie, ponawianie."
Teraz oprzemy swoje badania fraktali na dosyć prostym algorytmie:. Bierzemy jakikolwiek punkt P1 płaszczyzny X, wybieramy losowo jedną z transformacji Wk (k=1,2,..,n) poddajemy go jej działaniu otrzymując punkt P2. Proces ten powtarzamy (iterujemy) z punktem P2 by otrzymać współrzędne punktu P3 i etc. W rezultacie otrzymujemy ciąg punktów, który zbiega się do obiektu A będącego punktem stałym układu transformacji Wk. Kolejno wyliczane punkty Pi dosyć chaotycznie układają się w granicach zbioru A powoli ujawniając jego kształt. Gdyby transformacje Wk nie były zupełnie losowe można uzyskać cieniowanie obiektu. Odpowiednio dobierając parametry prawdopodobieństw transformacji Wk można uzyskiwać bardzo ciekawe efekty jak: zmiana oświetlenia, rozmycie krawędzi rozlanie barw, przenikanie kształtów itp.Mała galeria fraktali - (ze strony A. Krzysztofowicza - IF PAP Słupsk)
Literatura