Sparare a velocità di luce

Time dilation

 

Questo sperimento, con due spari – uno alla parete in quiete ed uno in movimento dimostra il concetto della dilatazione del tempo: i processi fisici negli sistemi di riferimento che si muovono sono più lenti che gli stessi processi in sistemi di riferimento in quiete.

 

La prima conferma sperimentale fu notata nell’allungamento di vita di muone, che in quiete vive 1.52 10^-6 s, ma con fasci di raggi cosmici veloci penetra molto più in profondità dell’atmosfera che li permetterebbe il tempo di vita “in quiete”. Viaggiando con 0.994 della velocità di luce, la sua vita si allunga - secondo i nostri orologi fino a 1.4 10^-5 s (9 volte di piu') -  l’orologio interno di muone in moto ritarda.

 

Il seguente sperimento illustra la causa di questo “ritardo” dell’orologio in moto (che secondo il principio di Einstein è sempre un moto relativo).

 

Il tempo viene misurato come intervallo tra il lancio ed l’arrivo dell’ impulso di luce (qui una pallina).

1. in quiete, la luce (pallina) percorre la distanza 2L, ed impiega tempo t=2L/v, dove v è la velocità della pallina

  

1. in moto, l’impulso (la pallina) mandata perpendicolarmente (in sistema di riferimento di lanciatore), si riflette lo stesso dalla parete bersaglio e torna al lanciatore (se anche dal punto di vista della parete, la pallina non arriva perpendicolarmente: l’angolo di riflessione e uguale all’angolo di impatto e pallina torna al lanciatore nonostante questo si muova)

 

 

Chiaro, che la pallina “2” percorre più strada.

 

Nel sistema classico, le due palline “1” ed “2” impiegano lo stesso tempo per tornare: la palina “2” pur percorrendo più strada lo fa con una maggiore velocità . Cioè, per la pallina “2”, alla sua velocità perpendicolare si somma la velocità “longitudinale” v_L, dando la somma v_somma=√(v²+v_L²). Così, pur avendo percorso più strada (l’ipotenusa del triangolo =√(4L²+t²v_L²)) il tempo impiegato rimane lo stesso t₁=√(4L²+t²v_L²)/√(v²+v_L²) = t

 

Nel caso relativistico, questa coincidenza d’arrivo  delle due palline non è più vera. Semplicemente, nessuna velocità può superare la velocità della luce e così v_somma=c. In conseguenza il tempo t che piega la pallina “2” per tornare si allunga – il fascio di luce, mandato allo specchio che si muove, arriva con un ritardo.

In dettaglio, assumendo la velocità della pistola v_L, il tempo impiegato dalla pallina per tornare equivale

 

t’=√(4L²+t’²v_L²)/c

 

e sostituendo L con  il tempo “in quiete” t=2L/c si ottiene

 

t’=t/ √[1-v_L²/c²]

 

 

 

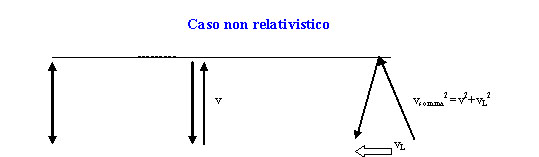
                 Pallina sparata dalla pistola in quiete       Pistola “2” si muove con v_L

                     distanza L                velocità della pallina v                            velocità totale della pallina v_somma=√(v²+v_L²)

                                        tempo   t=2L/v                                      tempo t₁=√(4L²+t²v_L²)/√(v²+v_L²) = t

     

 

 

                                                  

 

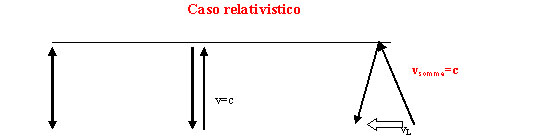
               Pallina sparata dalla pistola in quiete               Pistola “2” si muove con v_L

                    distanza L          velocità della pallina c                                    velocità totale della pallina rimane c

                                      tempo   t=2L/c                                              t’=√[(2L)²+(t’v_L)²]/c

 

           

 

Pallina sparata dalle pistola in moto: la strada percorsa =√[(2L)²+(t’v_L)² è maggiore che in caso “1”.

E se la velocità di moto della pallina (=luce) rimane c, il tempo impiegato è maggiore.

L’orologio posto su una parete in moto ritarda.