Orbitalna liczba kwantowa
Orbitalna
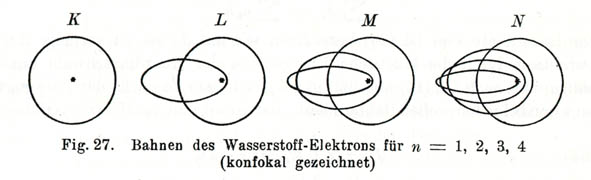
(azymutalna) liczba kwantowa k Sommerfelda określała spłaszczenie
orbity: krótsza półoś elipsy b określona
była przez wyrażenie b = a k/n, gdzie a jest półosią dłuższą a n – główną liczbą kwantową (tj. numerem
orbity u Bohra).


Współczesna mechanika kwantowa dla liczby kwantowej
l = 0 przewiduje
kuliste rozkłady
gęstości elektronów natomiast orbity wydłużone dla dużych wartości l.