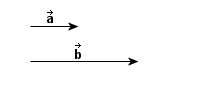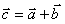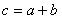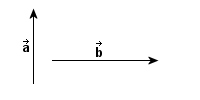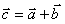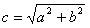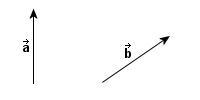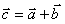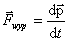

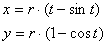
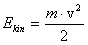
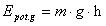
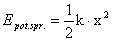
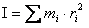
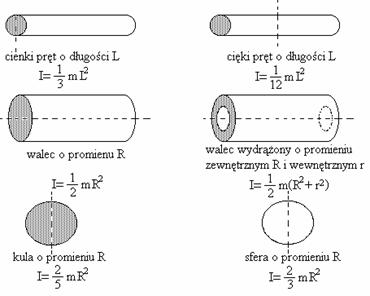
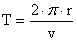
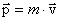
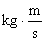
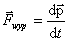
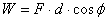
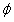 jest kątem
między kierunkami wektorów przemieszczenia
i siły.
jest kątem
między kierunkami wektorów przemieszczenia
i siły.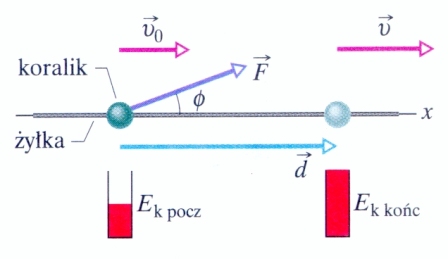
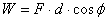

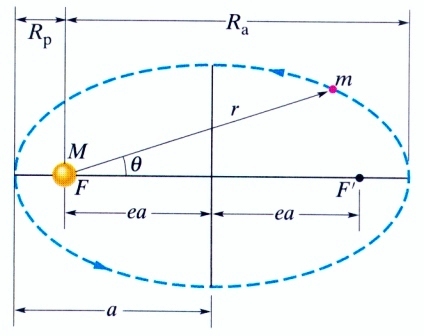
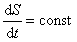
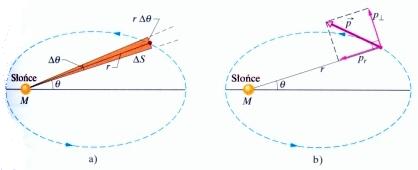
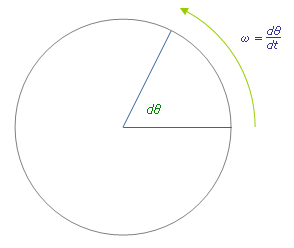
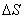 zakreślony przez kąt
zakreślony przez kąt 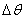 , który został
zatoczony
przez linię, łączącą planetę ze Słońcem o masie M w pewnym przedziale
czasu. b) Pęd
i składowe pędu danej planety.
, który został
zatoczony
przez linię, łączącą planetę ze Słońcem o masie M w pewnym przedziale
czasu. b) Pęd
i składowe pędu danej planety.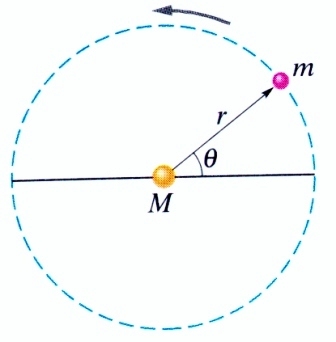
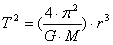
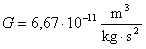
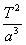
| planeta | półoś wielka a | Okres T | T²/a³ |
| Merkury | 5,79 | 0,241 | 2,99 |
| Wenus | 10,8 | 0,615 | 3,00 |
| Ziemia | 15 | 1 | 2,96 |
| Mars | 22,8 | 1,88 | 2,98 |
| Jowisz | 77,8 | 11,9 | 3,01 |
| Saturn | 143 | 29,5 | 2,98 |
| Uran | 287 | 84 | 2,98 |
| Neptun | 450 | 165 | 2,99 |
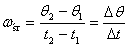
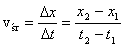
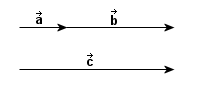
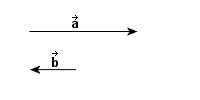
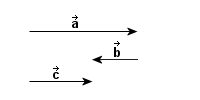
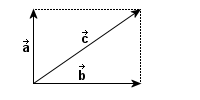
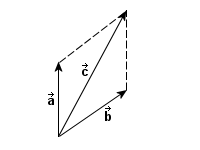
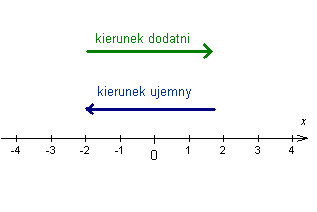
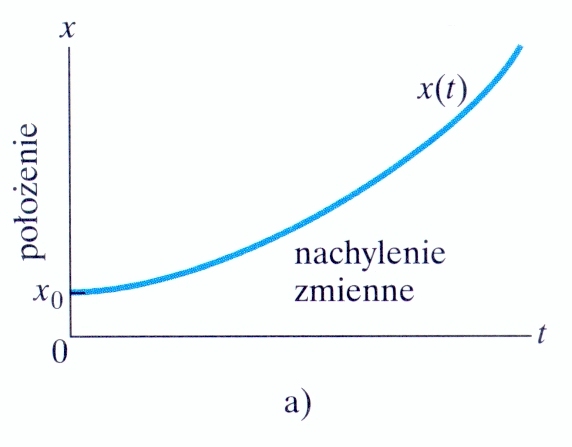
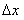 to wielkość wektorowa, która
opisuje zmianę położenia
punktu
to wielkość wektorowa, która
opisuje zmianę położenia
punktu 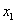 do innego punktu
do innego punktu 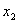 , przy czym zachodzi:
, przy czym zachodzi: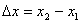
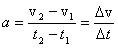
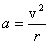
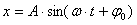
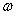 to częstość kołowa drgań. Okresem drgań harmonicznych
nazywamy najmniejszy odstęp czasu, po upływie którego powtarzają się
wartości wszystkich wielkości fizycznych charakteryzujących drganie.
Wyrażenie występujące pod znakiem funkcji sinus nazywamy fazą drgań
określającą wartość x w chwili t, a
to częstość kołowa drgań. Okresem drgań harmonicznych
nazywamy najmniejszy odstęp czasu, po upływie którego powtarzają się
wartości wszystkich wielkości fizycznych charakteryzujących drganie.
Wyrażenie występujące pod znakiem funkcji sinus nazywamy fazą drgań
określającą wartość x w chwili t, a 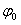 nazywamy
fazą
początkową
drgań,
która
określa wartość wielkości x w
chwili t = 0.
nazywamy
fazą
początkową
drgań,
która
określa wartość wielkości x w
chwili t = 0.
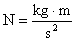
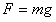
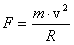
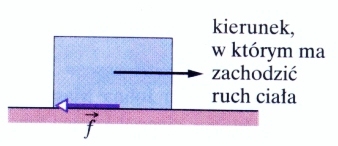
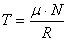
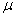 to
współczynnik tarcia tocznego.
to
współczynnik tarcia tocznego.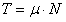
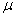 to
współczynnik tarcia statycznego, a N to wartość siły
normalnej.
to
współczynnik tarcia statycznego, a N to wartość siły
normalnej.